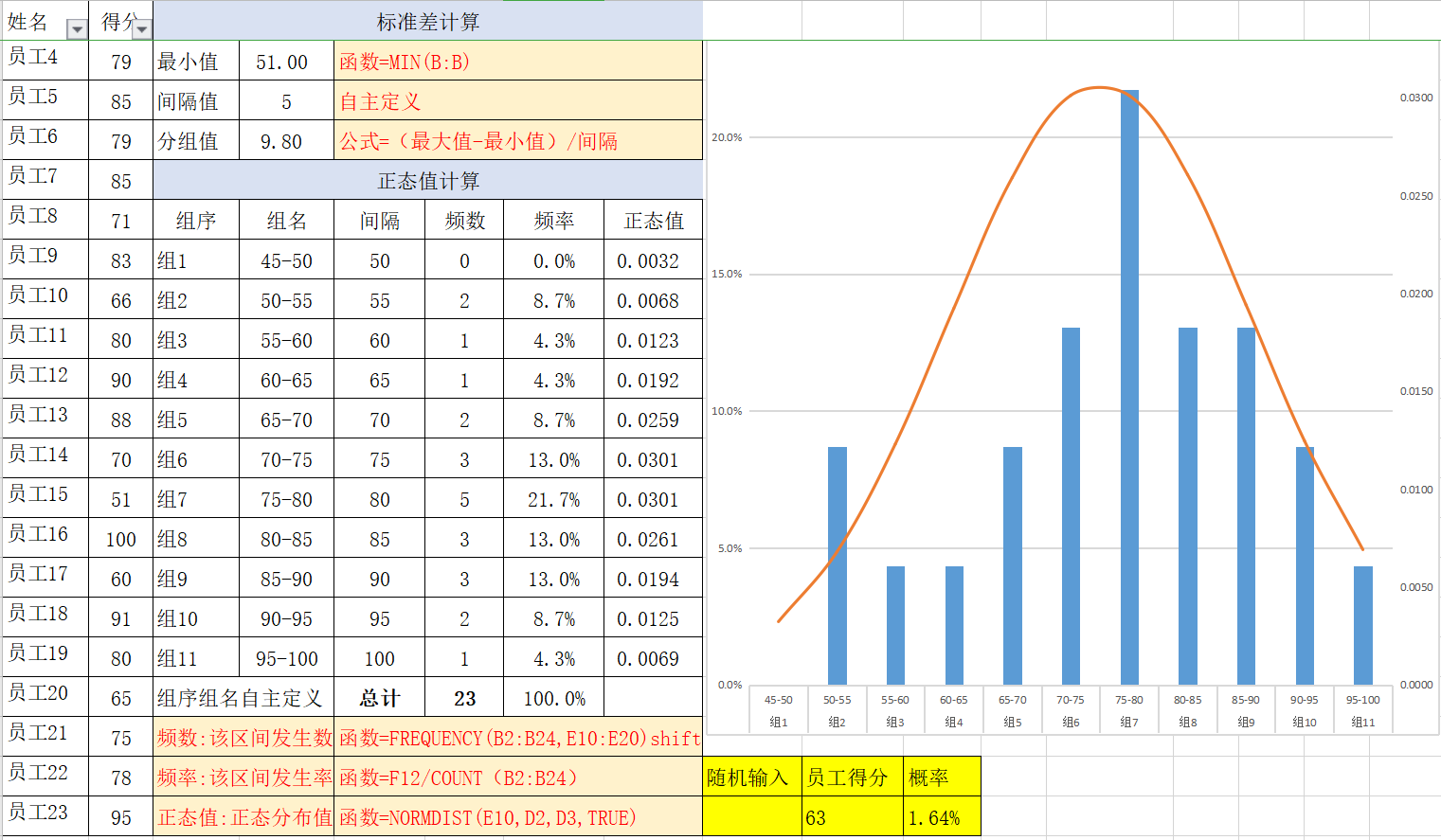
输入数据,根据模板可自动生成正态分布图。
| 频数:该区间发生数 | 函数=FREQUENCY(B2:B24,E10:E20)shift+ctrl+enter |
| 频率:该区间发生率 | 函数=F12/COUNT(B2:B24) |
| 正态值:正态分布值 | 函数=NORMDIST(E10,D2,D3,TRUE) |
大家都听过正态分布,这个名字不太直观,看英文Normal Distribution,normal就是正常的、标准的、常见的意思,其实翻译成“正常分布”会更好理解。
正态分布就是自然界中最常见的分布。
是统计学的基本理论分布。
对于同一总体画频率分布图,观察的样本逐渐增多,组段不断细分,直条的宽度逐渐变窄,最终顶端接近一条平滑的曲线,呈现为大部分集中在平均值附近,且越远离平均值出现频率越低,形成中间高两侧逐渐下降并对称的频率密度曲线,就是正态分布。
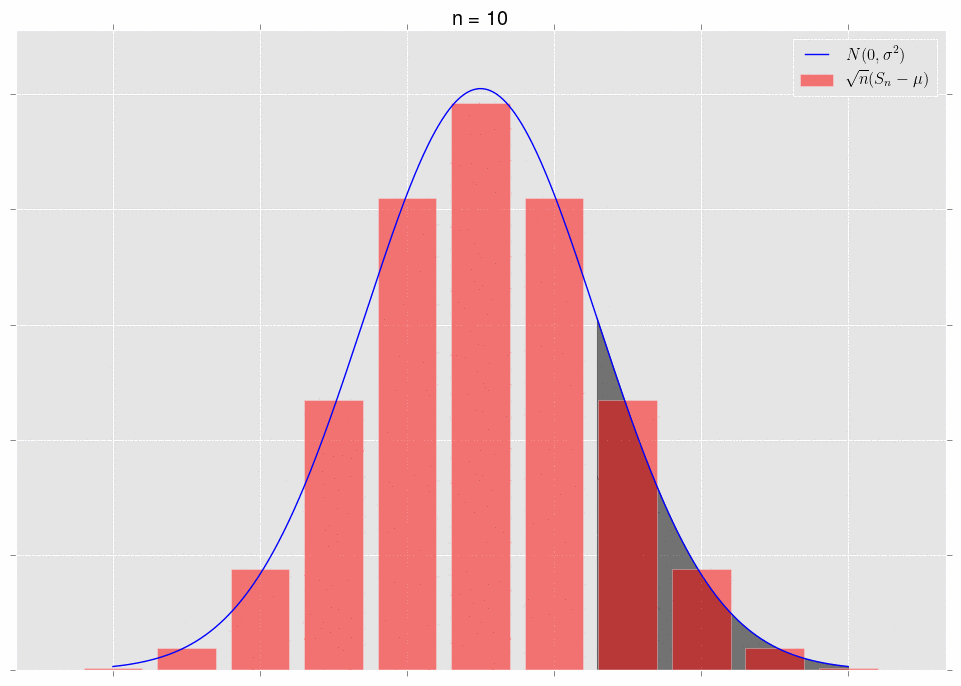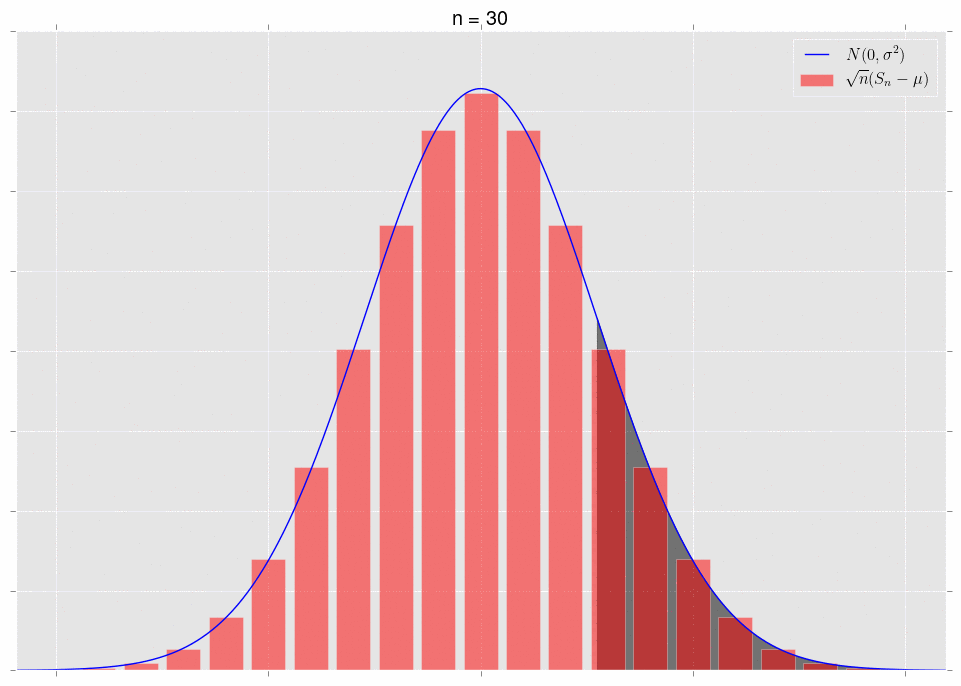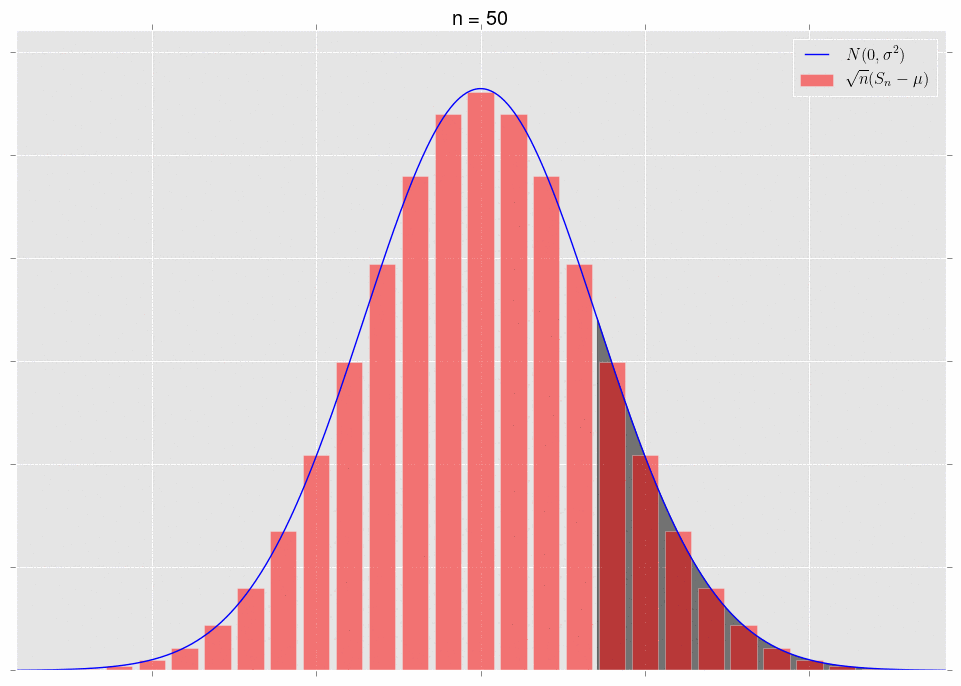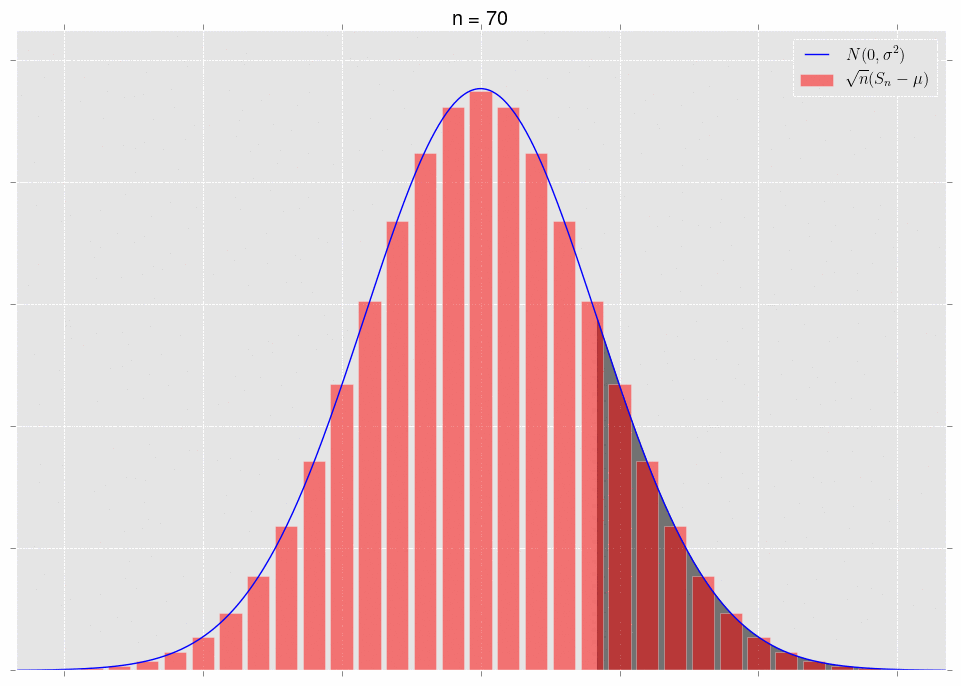
正态分布的频率密度曲线(直条的面积代表各组段的频率,直条的高度相当于频率除以组距,称为频率密度)

这个函数大家不用记,其他均为固定参数,我们只要知道正态曲线由均数(μ)和标准差(σ)决定,习惯上用N(μ,σ2)表示。当μ=0,σ=1时,称为标准正态分布。
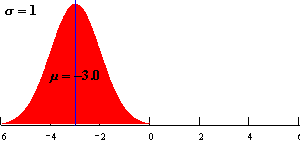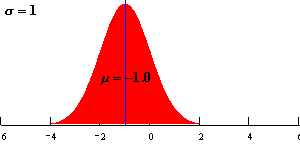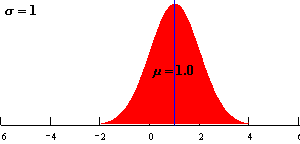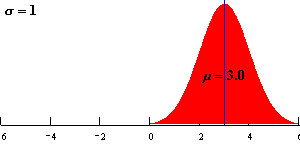
μ决定曲线在横轴的位置,μ增大曲线向横轴右移;μ减小曲线向横轴左移。
σ决定曲线形状,当μ固定时,σ越大,曲线越“矮胖”(数据越分散);σ越小,曲线越“瘦高”(数据越集中)。标准差是用来描述离散趋势的,标准差越大,数据越离散,那么曲线势必会变“矮胖”。

曲线关于μ对称,在μ处取得最大值。曲线下面积为“1”。1、68-95-99.7法则(正负1、2、3个标准差内曲线下面积)在μ±σ区间内(正负1个标准差范围内),面积占总体的68.27%。在μ±2σ区间内(正负2个标准差范围内),面积占总体的95.44%。在μ±3σ区间内(正负3个标准差范围内),面积占总体的99.74%。2、90-95-99%(曲线下面积为90、95、99%时对应标准差范围)
我们实际工作当中经常用到的曲线下面积有:90%、95%和99%,对应的位置为μ±1.64σ、μ±1.96σ和μ±2.58σ。之前说到百分位数可以用来制定医学参考值范围,均数标准差也可以,我们之后归纳专门讲解医学参考值范围是如何制定的。
我们在应用时不用管复杂的公式推导,只要主观上能判断即可:总体中每个个体变量为连续变量(近似连续变量),变量数值在一定范围内(有上、下界值)。由于变量的影响因素较多、随机、均匀作用于个体,即总体存在同质性;同时由于影响因素的多样、复杂最终个体会表现出变异性。因为同质性的存在,变量趋向聚集在均数附近(集中趋势);因为变异性的存在,变量会向着平均水平左右方向离散(离散趋势),最终频率分布呈现出中间高两侧逐渐下降并对称的“钟形”曲线。
这个条件说起来简单,但是大家要清楚我们统计学上的总体和通俗认为的总体根本不是一回事儿。统计学上的总体一定是根据观察变量而言的,同一总体内影响变量的因素较多、随机、均匀作用于每个个体,是产生正态分布的前提。我们医学科研当中设置纳入排除标准就是要明确总体范围。比如血压:如果你研究目的是全体人群,因为人类有普遍同质性存在。大部分人血压在正常范围内,少部分人的血压偏高或偏低,是符合正态分布的。但是如果你研究目的是高血压人群,那么就要纳入排除确定某一病理状态下人群为总体,那么在该总体下,大部分高血压会集中于某一血压范围,少部分人的血压相对于平均水平较高或较低,也是符合正态分布的。注意以上例子都是血压,但是总体却大相径庭,这点大家一定要注意。
比如说居民收入水平,大家都知道如果不规定特定总体,全国来看影响收入的因素并不是均匀作用于每一个人的,相应全人群收入肯定是不符合正态分布的。大家也能直观感受到用平均收入来描述平均水平根本不合理。光就收入而言,你我和马云们根本就不是一类“人”,不能放一起。我们之前介绍过离散/连续这一对概念,可以连续均匀在数轴上取值的为连续变量。比如身高、血压等,都是连续变量。那么近似连续变量是什么呢?就是虽然不能在数轴连续取值,但是取值要满足均匀且较多。比如最终是百分制,那么能够在1、2、3。。。100范围内都能取值,就可看成近似连续。但是同样是百分制,只能取10、20、30。。。100,那么虽然取值均匀了但是不够多。经验来看一般至少要超过10-20个取值,才有可能看做近似连续最终符合正态分布(具体要看正态检验)。举例2:医学当中常见的抗体滴度,是以几何形式变化的,不满足连续性,但是可以通过对数转化变成连续变量,这里不多赘述。在同一总体内,个体变量的值会由于同质性的作用趋向平均值,由于变异影响又会离开平均值,但是最终大部分会在一定范围内(比如均数±3个标准差范围内个体占总体的99.7%)。当然这个上下界值要结合专业去判断。如果说很多样本都在界值外,就要高度注意。通过以上三个感性判断条件,你就能排除很多不适用与正态分布的情况,请理解并掌握。医学科研当中满足正态分布的变量,一般标准差不超过均数的1/3或1/2。所以当你看到文章报告均数±标准差时,标准差接近甚至超过均数的,就要打个问号,统计方法是否有问题。
以上归纳的满足正态分布的条件虽然是主观判断但很实用,实际应用当中能帮助我们快速判断、把握,最终满足不满足正态分布是要做正态性检验的。
同一总体内,影响变量的因素较多、随机、均匀作用于每个个体,产生同质性、变异性,变量如果满足连续性,就会呈现集中于某一平均水平,并在一定范围内的正态分布。
内容未完全展示,请下载附件查看












